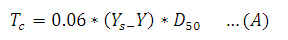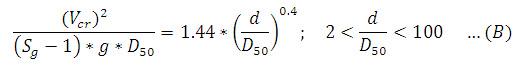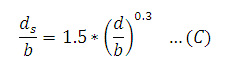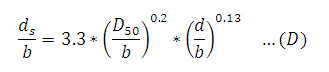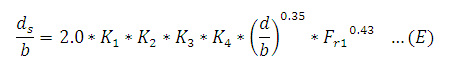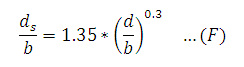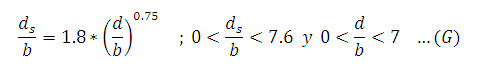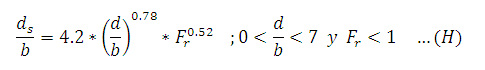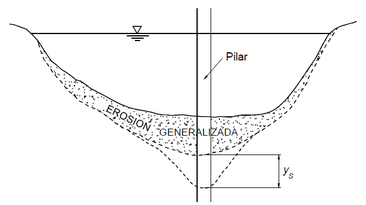
Socavación en Puentes

Introducción

De acuerdo a la Federal Highway Administration y a numerosos estudios de socavación realizados en los últimos decenios, la socavación en los estribos y pilares de los puentes ha sido, históricamente, la causa más importante de falla en estas estructuras.

Cuando los pilares de un puente se establecen en lechos erosionables, la alta velocidad local del flujo, causada por la interacción fluido-estructura, origina socavación a las zonas aledañas a los pilares, que gradualmente se extiende por debajo de ellos, eventualmente destruyéndolos.  Como ha sido reportado por muchos investigadores, como Lefter, Antunes y la Federal Highway Administration.

Concepto general de socavación y su relación con la erosión

La socavación puede definirse como la erosión “local” del lecho de un cauce natural.  En general, la erosión en un río consta de tres componentes: la erosión general, erosión en estrechamientos o transversal y erosión local o socavación; esta última es la que se debe a la interacción fluido-estructura en presencia de un material superficial erosionable, es la más importante.

En la siguiente figura, presentada por el Dr. Rocha en su libro “Introducción a la Hidráulica Fluvial” se muestra cómo la socavación se adiciona a la erosión general en un cauce natural.modificar.

Tipos de socavación

Según Juan Martín Vide, en su libro Ingeniería de Ríos, hay dos modalidades distintas de erosión local en pilares y estribos.

• En la primera, conocida como socavación en agua clara, la corriente no es capaz de poner en movimiento el material del lecho del río,  pero los vórtices si son capaces de socavar el pilar.  En este caso, al no haber arrastre de sedimentos del lecho desde aguas arriba, no hay reabastecimiento de materiales en el hueco socavado.
• En la segunda modalidad, conocida como socavación en lecho móvil, hay transporte de sedimentos del lecho desde aguas arriba hasta el sitio del puente y, por lo tanto, parte de este sedimento queda atrapado en el hueco de socavación.

Fórmulas para el cálculo de la profundidad de socavación

La profundidad de socavación es típicamente mucho mayor que la que resulta de la erosión general, según Fischenich y Landers, a menudo por un factor de 10.

Los investigadores han estudiado extensamente la profundidad de erosión local y han recomendado muchas fórmulas empíricas para los propósitos de predicción, pero los resultados de un pilar específico incluso para ecuaciones similares varían ampliamente.  Así, pues, tal como lo explican Shen, Raudkivi y Yanmaz, debido a la complejidad del proceso de socavación en ríos, el desarrollo de una relación matemática entre profundidad de socavación no es factible para condiciones universales.

La socavación se produce cuando el esfuerzo cortante en la interfaz de las partículas del flujo excede el valor crítico necesario para el movimiento de las partículas de sedimentos en la dirección del flujo.  Según muestra Neill en su libro “Guide to Bridge Hydraulics”, el esfuerzo cortante crítico puede ser calculado usando el criterio de Shields, como se muestra:

Donde Tc = esfuerzo crítico de corte (N/m2), Ys = peso específico de las partícula de sedimento (N/m3), Y = peso específico del agua (N/m3), y D50 = diámetro medio del grano (m), que debe ser mayor que 5 mm.

La velocidad crítica puede ser calculada usando la ecuación de Hanco.

Donde Vcr = velocidad umbral media (m/s), Mx = peso específico de los sedimentos, g = aceleración de la gravedad (m/s2).  Debido al vórtice de la herradura y la aceleración de la velocidad del flujo alrededor del pilar, la velocidad local adyacente al pilar es más grande que la velocidad aproximada del flujo de aguas arriba.  Neill sugiere la siguiente ecuación para calcular la profundidad de socavación, ds, en un pilar rectangular en condiciones de lecho vivo para α = 0:

Donde “α” es el ángulo de ataque.  Hanco (Breusers y otros, 1977) recomienda una ecuación para un caso general en el cual el tamaño de las partículas de los sedimentos son incluidos por d/b  > 1, y D50 = 0.5, 2, y 5 mm.

Una ecuación basada en la ecuación de Colorado State University (CSU) es sugerida para lecho vivo y la profundidad de socavación (Richardson y otros, 1990), que actualmente está en el manual de HEC-18 (SNS, 2001):

Donde K1 = factor de corrección por la forma de la nariz del pilar (1 para las narices redondeadas y 1.1 para las narices rectangulares), K2 = factor de corrección por el ángulo de ataque del flujo (1 para un ángulo de ataque de cero y un rango de L/b = 4 a 12, donde “L” es la longitud del pilar), K3 = factor de corrección por las condiciones del lecho (1.1 para la socavación de agua clara y 1 para la socavación de lecho vivo), K4 = factor de corrección de acorazamiento,  y Fr = número de Froude del flujo. En el manual de HEC-18, se pueden encontrar más detalles de la ecuación (E).

Veiga reportó la siguiente ecuación para estimar la profundidad de socavación en condiciones de socavación de un lecho vivo (o lecho móvil) de un pilar circular y 0.5 < d/b < 4, en la cual la influencia del tamaño de los granos es considerada como insignificante para D < 0.5mm en ds/b:

Una relación alternativa es dada por experimentos indios de modelos de pilares de puentes en un lecho arenoso con condiciones de socavación por lecho móvil (Laursen, 1962):

Hay otra ecuación experimental india expresada por Inglis (1949) en la cual el número de Froude es usando considerando lo siguiente:

Donde Fr es el número de Froude, que se puede expresar como.  Donde g = aceleración de la gravedad, y V = velocidad media del flujo. Las ecuaciones antes mencionadas representan solo algunos ejemplos de los muchos que se han derivado para predecir la profundidad en pilas de puentes.

Comparación de las fórmulas presentadas con mediciones hechas en campo

A fines de 2007, la universidad de Shahrekord, situada en la provincia de Fars, en Irán, realizó un estudio, donde se investigó el fenómeno de la socavación en nueve puentes, ubicados en cinco ríos, con un total de 37 pilares.  El estudio consistió en probar la bondad de las fórmulas más utilizadas en la estimación de la socavación en pilares y estribos de puentes con datos realmente medidos luego de avenidas extremas que se dieron entre los años que duró la investigación.  El tirante promedio aguas arriba fue determinado usando la información registrada por un limnígrafo y una curva de aforo disponibles para la sección del río.  Durante las investigaciones de campo, producto de una gran avenida que ocurrió en noviembre de 1986, tres de los nueve puentes colapsaron.  Estos fueron: Shir Baba, Keradeh y Ghotb-Abad, en los ríos Ardakan, Keradeh y Jahrom Salt respectivamente.

A partir de la investigación realizada por la universidad de Shahrekord, se pudo concluir que cuando el tamaño de partícula de los sedimentos aumenta, la profundidad de socavación disminuye.  Y, con respecto a las fórmulas de estimación de la socavación en pilares y estribos de puentes, la comparación estas con las medidas de campo revelaron que las ecuaciones de Hanco, CSU, Veiga y Neil exhibieron buen acuerdo con la información de campo; por otro lado, las ecuaciones de la India e Inglis sobreestimaron la profundidad de socavación.

Referencias

• BREUSERS, H.N.C., Nicollet, G. y Shen, H.W. (1997) Local Scour Around Cylindrical Piers. Journal of Hydraulic Research, IAHR
• CHOW, Ven Te (1959) Hidráulica de Canales Abiertos, McGraw- Hill, New York
• FEDERAL HIGHWAY ADMINISTRATION (FHWA) (1998) US Department of Transport, Bridge Technology, Summary of scanning review of European practice for bridge scour and stream instability countermeasures (http://www.fhwa.dot.gov/bridge/scan-txt.htm)
• GHORBANI, Behzad (2007) A Field Study of Scour at Bridge Piers in Flood Plain Rivers. Water Engineering Department, College of Agriculture, Shahrekord University, Fars - Irán
• INGLIS, S.C. (1949) The Behaviour and Control of Rivers and Canals. Research Publ. No. 13, Central Water Power Irrigation and Navigation Report, Poona Research Station, India
• FISCHENICH, C. and Landers, M. (2000) Computing Scour 2000. Technical Notes Collection, U.S. Army Engineering. Research and Development Center, Vicksburg, MS: (http://www.wes.army.mil/el/emrrp/pdf/sr05.pdf)
• HENDERSON, F.M. (1996) Open Channel Flow. Macmillan, New York
• LAURSEN, E.M. (1962) Scour at Bridge Crossings. Trans. ASCE Vol. 127, part 1, p.166
• NEILL, C.R. (1975) Guide to Bridge Hydraulics. Project Committee on Bridge Hydraulics of RTAC, University of Toronto Press, Canada
• NATIONAL HIGHWAY INSTITUTE (NHI) (2001) Evaluating Scour at Bridges. Hydraulic Engineering Circular No. 18, 4th edition, Publication No. FHWA NHI 01-001, US Dept. of Transportation, Federal Highway Administration
• ROCHA, Arturo (1998) Introducción a la Hidráulica Fluvial. Facultad de Ingeniería Civil – Universidad Nacional de Ingeniería (FIC-UNI), Lima
• ​VIDE, Juan Martín (2003) Ingeniería de Ríos. Alfaomega Grupo Editor: Cataluña